昨天介紹了 Extended Binary Tree，今天要來介紹求 WEPL 的演算法。

霍夫曼演算法（Huffman Algorithm）

1. 令 W = external node 加權值集合
2. 從 W 中取出兩個加權值，建立 Extended Binary Tree
3. 將此 2 個加權值相加後放回 W 中
4. 重複 2 3 步驟，直到 W 中剩下一個 value

示範：假設 W = {2, 3, 5, 7, 9, 13}

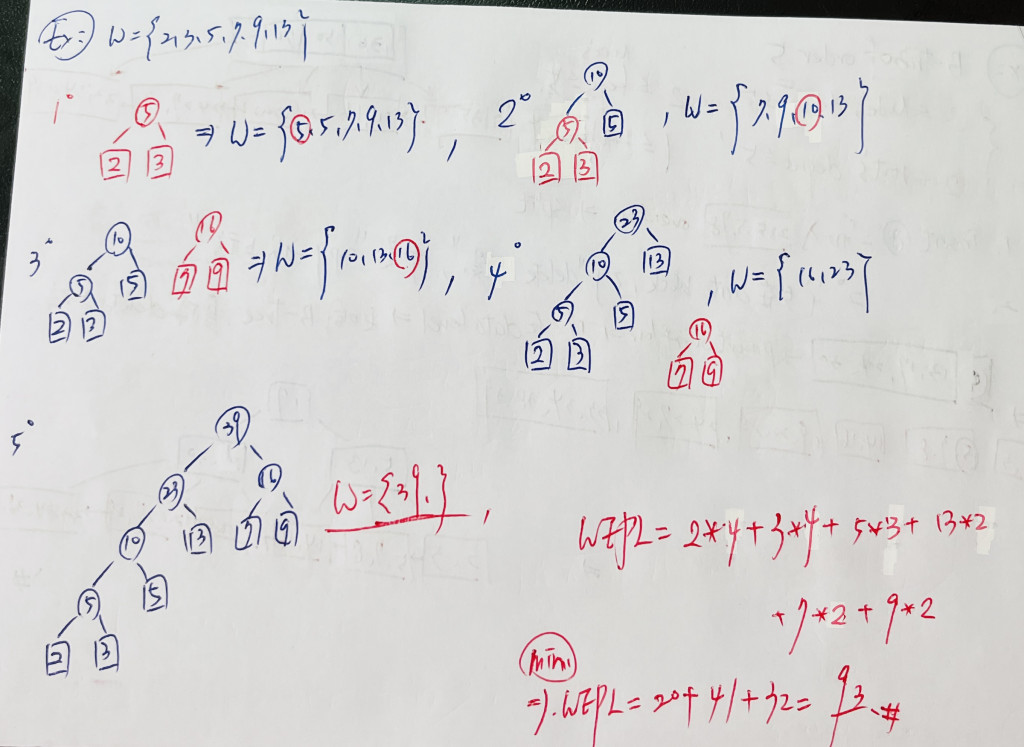
而這棵樹又叫做 Huffman Tree，而其一定是 Strict Binary Tree

我們來分析一下這個演算法的時間複雜度：

1. 因為會對 W 做 n - 1 次的 delete-min，及 n - 1 次的 insert。因此 W 使用 min-heap 來維護最有效率。
2. 而總共做 3 * (n - 1) 次 O(logn)的動作。演算法的時間複雜度 = O(nlogn)

Huffman code

將資料建立成 huffman tree 後，向左的 link 為 0，向右的 link 則為 1。
外部節點放的是資料出現的頻率，因此從 root 開始走到該資料路徑中的 0 或 1，就是那個資料的編碼。

這個編碼有個特性，叫做 prefix code，也就是，每個編碼不可能會在其他訊息中的前綴中出現，也就是說解碼可以很好判斷，不會判斷錯。

用一個例子來看看：176 次的 message。
出現次數：a(12)、b(3)、c(57)、d(51)、e(33)、f(20)，請問各訊息編碼？共需幾個 bits 表示？平均編碼長度？與固定編碼系統比，省下多少空間？

Greedy Algorithm

Huffman code 可以展示一個重要的演算法觀念：greedy algorithm
也就是用直覺去思考，如何達成最佳解。
要讓 WEPL 最小，就要將加權值大的放的離 root 近，加權值小的放的離 root 遠
所以挑選當下的最佳解，也就是兩個最小值來建立 Huffman Tree

但 Greedy Algorithm 不一定保證全域的最佳解，例如：0/1 背包問題，就必須要用 Dynamic programming 求解。差別就在於 Greedy 只看未來情況判斷當下最佳解，Dynamic Programming 則是會將過去資料運用表格儲存，並重複使用得到整個問題的最佳解。